2 Section 1.2: Reading Music

Reading music is hard, at first. Just like any new skill, it takes practice, patience, and a tenacious attitude to keep moving forward. Using the tools given to you in the first section you can practice reading music until you feel comfortable looking at a score or grand staff. One of the most important tools in sight-reading and music performance is the ability to identify how a composer has strung the building blocks of music such as rhythm, melody, and harmony together in order to create one whole piece of art. Before one can achieve that they must first master the use of each component of rhythm, harmony, and melody individually.

INTERVALS

An INTERVAL is defined in Mathematics as the distance between two points. In music, we use the term in the same manner but the two points in question are musical tones instead of points on a graph. So, for musicians, the term INTERVAL means the space between two notes. Intervals are transmitted graphically in two different ways, which means they have two different textures of sound with which the theory student should become familiar.

When two tones are sounded separately but close enough to another tone to infer a melodic relationship, we label them MELODIC. When two tones are sounded together as an incomplete chord we say they are HARMONIC because they infer a harmony or multiple harmonies. Melodic intervals have a specific TIMBRE or tone quality to them that can be identified after practice with and without a piano keyboard. Harmonic intervals also have a specific tone quality or timbre that is identifiable as well. The tones used in the example above are F and C. Sit down at the piano and play these two notes wherever you can find them on a keyboard. For reference, the F note is the first white note before the group of three black keys. The C note is the first white key before the group of two black keys. A mathematical pattern that is true the length of the entire piano keyboard.

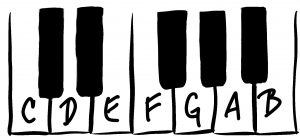
Listen to each separately and together. Listen to how they react to each other in both fields, but don’t try to just memorize the sound, attempt to absorb it. Spend as much time as you can with the same interval until you can recognize it everywhere, until it becomes part of your vocabulary, until you cannot forget it.

The first interval we will study is called the UNISON. This is very basic as you can see in the example below, two different voices or sounds supply the same pitch or note in the same range.

The next intervals we study will be useful in every aspect of music theory application. They will be the tools we use to identify complex melodic and harmonic motion. The first one is referred to as the HALF-STEP. The Half-Step can be found on the piano keyboard when moving from white key to black key and vice versa. There are only two places on the keyboard in which this formula deviates: between the notes E and F and between B and C we call these Naturally Occurring Half-Steps. These spaces have NO black note between them and therefore are only one HALF-STEP apart from one another.

Notice in the example below, that notes E and F are naturally occurring half steps in graphic form. Play them together and separate to find the timbre of each until you cannot forget it.

ONE HALF-STEP

Now that we can see and hear a HALF-STEP move to the next logical interval, the WHOLE-STEP. Obviously, if we add two HALF-STEPS together we get one WHOLE-STEP. This is easy to see when dealing with White note to Black Note movement on a piano keyboard but what happens when we need a WHOLE-STEP away from E and need to RAISE the pitch F to fit a particular pattern. We use a symbol called an ACCIDENTAL. More specifically, a particular accidental is referred to as a SHARP. This alteration gives us F sharp, which is the first Black key in the pattern of three that lay across the length of the entire keyboard. Since we have NATURALLY OCCURING HALF STEPS between “E” and “F” we use the SYMBOL to the left of the tone to instruct the performer to raise the pitch F to F SHARP. Musicians refer to this as a WHOLE-STEP because raising the F to F sharp lengthens the musical space between the tones because we added two HALF-STEPS together.

ONE WHOLE-STEP 

We should pause our discussion of intervals here momentarily to discuss the SYMBOLS we call ACCIDENTALS. It will be of the utmost importance when we begin to study complex intervals and chords later in the book. Don’t worry we will be back in no time.

ACCIDENTALS

When we need a way to graphically alter notes to fit a pattern, we need to differentiate one from another by using certain symbols. Since patterns tend to repeat and shift at different times, the use of graphic representation to alter notes to fit these patterns or formulas is necessary. These situations that occur in music notation require an extension or redefinition of a musical tone, either for musical grammar and syntax, or mathematical patterns that occurs require the use of symbols called ACCIDENTALS.

Sharp – raises a tone one half step

Flat – Lowers a tone one half step

Natural – restores a note to its original placement

There are also extensions of this system as well, referred to as DOUBLE SHARP and DOUBLE FLAT. Very rarely will a performer see these in standard notation. These tools occur when composers have written very difficult music that moves in awkward patterns and there is a need for the symbol.

Double Sharp raises a tone two half steps

Double Flat lowers a tone two half steps

INTERVALLIC CLASSIFICATION AND APPLICATION

Intervals in music are identified by number and how many letter names span the defined space. However, we require modifiers for some musical situations to define a certain sound or specialty interval required to fit our pattern building, construction, and function. We call these MAJOR, MINOR, AUGMENTED, DIMINISHED, and PERFECT. We use an uppercase “M” to denote a MAJOR interval, we use a lower case “m” to denote a minor interval. We use an “A” to denote an augmented interval and “D” to denote a diminished interval. The PERFECT intervals have a “P” in front of them to denote their status. There are two areas of intervals with which the musician should become familiar.

AREA 1: Unisons, 4ths, 5ths, and octaves which are PERFECT intervals.

AREA 2: 2nds, 3rds, 6ths, and 7ths which are IMPERFECT intervals that need a modifier to tell us how they function.

Some intervals get the label of “STABLE” intervals because they give the impression of harmonic stability. This reveals something we refer to as CONSONANCE in music theory study. Simply put, consonance is the AGREEMENT of musical tones. This is what non-musicians hear and refer to as a good sound. The “UNSTABLE” intervals are referred to as DISSONANT intervals because they give the impression that there is an expected harmonic movement waiting to occur.

The first area of intervals referred to as PERFECT has a special relationship to each other that supply a specific texture but reveal no tonal quality. In other words, no musician will ever refer to perfect 5th as major or minor, always P for perfect. Intervals from Area 2 demonstrate tonality with respect to a major or minor scale, therefore they reveal the tonal quality of a specific harmonic area without being an actual harmony.

Minor 2nd: the minor second is synonymous with what is known as the half-step.

Major 2nd: the major second is also known as a whole-step, or the first two notes of a major scale.

FLAVOR

The next two intervals are very important in demonstrating what musicians sometimes call the “flavor” of a chord or harmony because they denote whether the harmony is MAJOR or MINOR. Musicians use the word flavor to describe the sound of chords and harmony because there are so many different tonal combinations that exist. The theory student will encounter a number of chords that have various functions based on their level of dissonance within a given tonal area. The 3rd is the most important part of a scale and a chord because it defines a specific tonal area.

Minor 3rd is three half-steps, or the third degree of a minor scale.

Major 3rd is four half-steps, or the third degree of a major scale.

Perfect 4th is five half-steps, or the fourth degree of a major or minor scale.

Perfect 5th is seven half-steps, or the fifth degree of a major or minor scale.

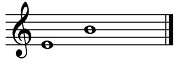
Minor 6th is eight half-steps, or the sixth scale degree of a natural minor scale.(pg33)

Major 6th is nine half-steps, or the sixth scale degree of a major scale.

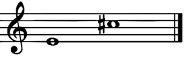
Minor 7th is ten half-steps, or the seventh scale degree in a natural minor scale.

Major 7th is eleven half-steps, or the seventh scale degree in a major scale.

Perfect 8th (octave); is twelve half-steps.

The perfect intervals can be expanded and retracted as well as the imperfect intervals. When this occurs, they should be referred to as Augmented if the space between them is lengthened and DIMINISHED if the space between them is shortened.

Augmented 5th is eight half-steps.

Diminished 5th is six half-steps.

Augmented 4th is also six half-steps.

Diminished 4th is five half-steps.

Note the similarities between the d5th and the A4th. These are also known by another label, the TRI-TONE. The tri-tone divides the octave mathematically into perfect halves. Aurally these intervals are the same, however, there is a large difference in function and application in various places throughout the study of music theory which will be discussed in the section covering harmony. Also, notice the similarity between the d4th and the major 3rd. 

INTERVALS MOVE IN TWO WAYS

Just as intervals go up, they can go down. In other words, intervallic relationships can be measured down from a base pitch as easily as they can be measured up from a base pitch. Count the corresponding intervals’ half steps down to find the desired interval.

Minor 2nd down (m2)

Major 2nd down (M2)

Minor 3rd down (m3)

Major 3rd down (M3)

Perfect 4th down (P4)

Perfect 5th down (P5)

Minor 6th down (m6)

Major 6th down (M6)

Minor 7th down (m7)

Major 7th down (M7)

Octave down (perfect)

All intervallic sounds should be memorized. This means an ample amount of time spent at the piano keyboard playing and singing these intervals. Participating in Active listening. Active Listening is an exercise in which the student puts all other distractions away and focuses simply on the interval to be internalized. The good student doesn’t practice until they get it right, they practice until they can’t get it wrong.

When a composer flips the arrangement of an interval by transferring it to another octave, it changes the intervallic relationship with respect to the other notes that surround it. When applied to the 2nd, 3rd, 4th, and 6th they give us new sounds within the same harmony called compound intervals. These new intervals are referred to as compound intervals because they travel past the next mathematical occurrence of the lowest note widening the interval to a large margin. They are the 9th, 10th, 11th, and 13th. These new intervals correspond to previously studied intervals when they were placed next to the root. However, if displaced up an octave the 2nd becomes a 9th, the 3rd becomes 10th, perfect 4th becomes an 11th, and a 6th becomes a 13th.

9th                  10th                  11th               13th

INTERVAL INVERSION

As noted previously, when a composer flips an interval to another octave, it impacts the relationship of that note with respect to the other notes that surround it. All intervals have an inverse that sounds and functions differently. They can be inverted or flipped upside down. For example, when a perfect 4th is inverted it becomes a perfect 5th and vice versa.

The key to inverting intervals is remembering two things:

1. If the beginning interval is major, its reciprocal will be minor and vice versa.
2. To get the desired inversion subtract the first number from 9. To double-check yourself add the remainder to the original interval if the total is 9 then you have calculated correctly.

Practice this exercise with the intervallic examples provided. Use the simple formula to double-check your work and then go find them on the keyboard.

Learning to identify intervals by sight and sound is a large part of the active professional musicians’ toolbox. Sight-reading is a requirement for independent contractors because they will play many different types of gigs in a short amount of time. This means they won’t have time to sit in the practice room and practice in the classical sense. They may have to take a pencil and begin to mark the road map and identify any potential problems and analyze the music to determine what is required. A thorough understanding of intervals is always in progress no matter how far you think you have come. The author of this text presently studies intervals on a daily basis in some form. So, don’t stop, ever.

TEXTURES

Music can be written in a variety of textures to portray a particular emotion, story or event within the grand scheme of music. There are four main textures with which the music student should be familiar:

• Monophonic – music that only has one melody performed by one instrument or voice, thus the prefix of mono is added to phonic meaning one sound or melody.
• Polyphonic – music that has many voices or instruments moving in several different directions simultaneously, thus poly a prefix meaning many things at the same time is added to phonic to denote several voices or instruments all moving musically in different directions.
• Homophonic – this music is the combination of multiple voices or instruments performing the same melody at the same time, thus the prefix homo means one melody added to phonic to include many voices.
• Heterophonic – this texture is a traditional style of music performance in which a chord or harmony is used to support a melody like a piano player. Two different things happen simultaneously, thus the prefix Hetero meaning two added to phonic.

DYNAMICS

Dynamics or Amplitude for musicians is equivalent to volume for the layperson. Studying music means spending time learning the symbols that represent dynamics in written music and the subtleties that come with them.

P is an abbreviation for the Italian word PIANO. When we use the P, we denote passages that are to be performed in a quiet manner. A composer may wish to use multiple P markings to make something very, very soft.

Piano Dynamic

Pianissimo Dynamic

Pianississimo Dynamic

In the event a composer wishes for the performer to be loud an F is used. This is short for FORTE in Italian. A composer may wish to use multiple F’s to inform the performer to be as loud as possible.

Forte Dynamic

Fortissimo Dynamic

Fortississimo Dynamic

There are points in between loud and soft music that must be addressed through dynamics. When composers wish for a passage to be moderately loud or moderately soft they put an M in front of P or F. M is short for MODERATO in Italian indicating a comfortable or “moderate” level of performance volume.

Mezzo Forte Dynamic

Mezzo Piano

Even though the system of communication is straightforward, each composer throughout music history and the present has their own interpretation of volume and what it means. For instance, Beethoven was passionate in his beliefs no matter what the subject. It could be said he was one of the most intense personalities in the history of Western music. That means his dynamic markings are an extension of an emotion he felt during that moment. As performers, we must know these things in order to portray the intended emotion as accurately as possible.

From a technical stance, subtle soft notes with good pitch centers are hard to achieve without steady practice. The same can be said for very loud notes. Many believe loud means ugly and this could not be more wrong. Loud still requires good tone and pitch. So, it is up to you to find those “sweet spots” of quiet intensity or uproarious volume during practice on your main instrument. Finding them enough times consistently that they become part of your vocabulary and not a “trick” you use to sound musically mature. Whatever instrument one chooses, all have techniques required for good tone at various amplitudes or volumes.

ARTICULATION

The word Articulate means to speak, utter or pronounce in a particular manner that is easily understood. For musicians, it is no different. Articulations are symbols we apply to notes to show a performer how a note should be shaped.

A note with a small dot over it tells the performer to play short and separated.

Notes with his mark are to be performed smooth and connected.

A note with a line over it tells the performer to give the note weight or emphasis.

A note with this symbol means to give the note an accent slightly above the written dynamic.

Sometimes we use two articulations together to form a new musical direction for the performer.

When a musician refers to the SHAPE of a note we are talking about how the note is physically initiated or “attacked”,  plus everything in between and the end or “release” of a note. In the area of Acoustic Theory, this is referred to as the envelope or the shape of a musical note.

Acoustic instrumentalists can alter the shape of a tone by using various means supplied to them by the usage of air, muscles of the jaw and lip areas, and the instrument itself. This is hard to achieve without regular practice. In order to achieve ultimate control over articulation for any instrument, one must use articulations as workouts. Using a metronome at a very slow tempo, take a specific articulation and perform it over and over until it becomes a natural sensation within your muscle group. Once you can attain regularity with quality, begin to slowly speed up the metronome 4-5 clicks at a time. When this is accomplished, we add another element. We slow the metronome back down and add dynamics to the equation. Perform the articulation at various dynamic levels to understand how different ranges feel and require different performance practices for different levels of dynamics. The student can also pick a dynamic and run various articulations in the same manner and get the same effect. The biggest lesson here is that composers write specific musical instructions such as dynamics and articulation for the performance of their music. We can be more prepared for any musical situation that arises if this type of practice is part of our everyday routine.