9 Chapter 9. Problem-Solving

CHAPTER 9: PROBLEM SOLVING 

How do we achieve our goals when the solution is not immediately obvious? What mental blocks are likely to get in our way, and how can we leverage our prior knowledge to solve novel problems?

CHAPTER 9 LICENSE AND ATTRIBUTION

Source: Multiple authors. Memory. In Cognitive Psychology and Cognitive Neuroscience. Wikibooks. Retrieved from https://en.wikibooks.org/wiki/ Cognitive_Psychology_and_Cognitive_Neuroscience

Wikibooks are licensed under the Creative Commons Attribution-ShareAlike License.

Cognitive Psychology and Cognitive Neuroscience is licensed under the GNU Free Documentation License.

Condensed from original version. American spellings used. Content added or changed to reflect American perspective and references. Context and transitions added throughout. Substantially edited, adapted, and (in some parts) rewritten for clarity and course relevance.

Cover photo by Pixabay on Pexels.

Knut is sitting at his desk, staring at a blank paper in front of him, and nervously playing with a pen in his right hand. Just a few hours left to hand in his essay and he has not written a word. All of a sudden he smashes his fist on the table and cries out: “I need a plan!”

Knut is confronted with something every one of us encounters in his daily life: he has a problem, and he does not know how to solve it. But what exactly is a problem? Are there strategies to solve problems? These are just a few of the questions we want to answer in this chapter.

We begin our chapter by giving a short description of what psychologists regard as a problem. Afterward we will discuss different approaches towards problem solving, starting with gestalt psychologists and ending with modern search strategies connected to artificial intelligence. In addition we will also consider how experts solve problems.

The most basic definition of a problem is any given situation that differs from a desired goal. This definition is very useful for discussing problem solving in terms of evolutionary adaptation, as it allows us to understand every aspect of (human or animal) life as a problem. This includes issues like finding food in harsh winters, remembering where you left your provisions, making decisions about which way to go, learning, repeating and varying all kinds of complex movements, and so on. Though all of these problems were of crucial importance during the human evolutionary process, they are by no means solved exclusively by humans. We find an amazing variety of different solutions for these problems in nature (just consider, for example, the way a bat hunts its prey compared to a spider). We will mainly focus on problems that are not solved by animals or evolution; we will instead focus on abstract problems, such as playing chess. Furthermore, we will not consider problems that have an obvious solution. For example, imagine Knut decides to take a sip of coffee from the mug next to his right hand. He does not even have to think about how to do this. This is not because the situation itself is trivial (a robot capable of recognizing the mug, deciding whether it is full, then grabbing it and moving it to Knut’s mouth would be a highly complex machine) but because in the context of all possible situations it is so trivial that it no longer is a problem our consciousness needs to be bothered with. The problems we will discuss in the following all need some conscious effort, though some seem to be solved without us being able to say how exactly we got to the solution. We will often find that the strategies we use to solve these problems are applicable to more basic problems, too.

Non-trivial, abstract problems can be divided into two groups: well-defined problems and ill- defined problems.

WELL-DEFINED PROBLEMS

For many abstract problems, it is possible to find an algorithmic solution. We call problems well-defined if they can be properly formalized, which involves the following properties:

•        The problem has a clearly defined given state. This might be the line-up of a chess game, a given formula you have to solve, or the set-up of the towers of Hanoi game (which we will discuss later).

•        There is a finite set of operators, that is, rules you may apply to the given state. For the chess game, e.g., these would be the rules that tell you which piece you may move to which position.

•        Finally, the problem has a clear goal state: The equations is resolved to x, all discs are moved to the right stack, or the other player is in checkmate.

A problem that fulfils these requirements can be implemented algorithmically. Therefore many well-defined problems can be very effectively solved by computers, like playing chess.

ILL-DEFINED PROBLEMS

Though many problems can be properly formalized, there are still others where this is not the case. Good examples for this are all kinds of tasks that involve creativity, and, generally speaking, all problems for which it is not possible to clearly define a given state and a goal state. Formalizing a problem such as “Please paint a beautiful picture” may be impossible.

Still, this is a problem most people would be able to approach in one way or the other, even if the result may be totally different from person to person. And while Knut might judge that picture X is gorgeous, you might completely disagree.

The line between well-defined and ill-defined problems is not always neat: ill-defined problems often involve sub-problems that can be perfectly well-defined. On the other hand, many everyday problems that seem to be completely well-defined involve — when examined in detail — a great amount of creativity and ambiguity. Consider Knut’s fairly ill-defined task of writing an essay: he will not be able to complete this task without first understanding the text he has to write about. This step is the first subgoal Knut has to solve. In this example, an ill-defined problem involves a well-defined sub-problem

RESTRUCTURING: THE GESTALTIST APPROACH

One dominant approach to problem solving originated from Gestalt psychologists in the 1920s. Their understanding of problem solving emphasizes behavior in situations requiring relatively novel means of attaining goals and suggests that problem solving involves a process called restructuring. With a Gestalt approach, two main questions have to be considered to understand the process of problem solving: 1) How is a problem represented in a person’s mind?, and 2) How does solving this problem involve a reorganization or restructuring of this representation?

HOW IS A PROBLEM REPRESENTED IN THE MIND?

In current research internal and external representations are distinguished: an internal representation is one held in memory, and which has to be retrieved by cognitive processes, while an external representation exists in the environment, such like physical objects or symbols whose information can be picked up and processed by the perceptual system.

Generally speaking, problem representations are models of the situation as experienced by the solver. Representing a problem means to analyze it and split it into separate components, including objects, predicates, state space, operators, and selection criteria.

The efficiency of problem solving depends on the underlying representations in a person’s mind, which usually also involves personal aspects. Re-analyzing the problem along different dimensions, or changing from one representation to another, can result in arriving at a new understanding of a problem. This is called restructuring. The following example illustrates this:

Two boys of different ages are playing badminton. The older one is a more skilled player, and therefore the outcome of matches between the two becomes predictable. After repeated defeats the younger boy finally loses interest in playing. The older boy now faces a problem, namely that he has no one to play with anymore. The usual options, according to M. Wertheimer (1945/82), range from “offering candy” and “playing a different game” to “not playing at full ability” and “shaming the younger boy into playing.” All of these strategies aim at making the younger boy stay.

The older boy instead comes up with a different solution: He proposes that they should try to keep the birdie in play as long as possible. Thus, they change from a game of competition to one of cooperation. The proposal is happily accepted, and the game is on again. The key in this story is that the older boy restructured the problem, having found that his attitude toward the game made it difficult to keep the younger boy playing. With the new type of game the problem is solved: the older boy is not bored, and the younger boy is not frustrated. In some cases, new representations can make a problem more difficult or much easier to solve. In the latter case insight– the sudden realization of a problem’s solution – may be the key to finding a solution.

INSIGHT

There are two very different ways of approaching a goal-oriented situation. In one case an organism readily reproduces the response to the given problem from past experience. This is called reproductive thinking.

The second way requires something new and different to achieve the goal—prior learning is of little help here. Such productive thinking is sometimes argued to involve insight. Gestalt psychologists state that insight problems are a separate category of problems in their own right.

Tasks that might involve insight usually have certain features: they require something new and non-obvious to be done, and in most cases they are difficult enough to predict that the initial solution attempt will be unsuccessful. When you solve a problem of this kind you often have a so called “aha” experience: the solution pops into mind all of a sudden. In one moment you have no idea how to answer the problem, and you feel you are not making any progress trying out different ideas, but in the next moment the problem is solved.

For readers who would like to experience such an effect, here is an example of an insight problem: Knut is given four pieces of a chain; each made up of three links. The task is to link it all up to a closed loop. To open a link costs 2 cents, and to close a link costs 3 cents. Knut has 15 cents to spend. What should Knut do?

If you want to know the correct solution, turn to the next page.

To show that solving insight problems involves restructuring, psychologists have created a number of problems that are more difficult to solve for participants with previous experiences, since it is harder for them to change the representation of the given situation.

For non-insight problems the opposite is the case. Solving arithmetical problems, for instance, requires schemas, through which one can get to the solution step by step.

FIXATION

Sometimes, previous experience or familiarity can even make problem solving more difficult. This is the case whenever habitual directions get in the way of finding new directions – an effect called fixation.

FUNCTIONAL FIXEDNESS

Functional fixedness concerns the solution of object use problems. The basic idea is that when the usual function an object is emphasized, it will be far more difficult for a person to use that object in a novel manner. An example for this effect is the candle problem: Imagine you are given a box of matches, some candles and tacks. On the wall of the room there is a cork-board. Your task is to fix the candle to the cork-board in such a way that no wax will drop on the floor when the candle is lit. Got an idea?

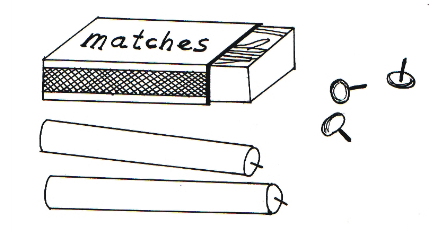
Here’s a clue: when people are confronted with a problem and given certain objects to solve it, it is difficult for them to figure out that they could use the objects in a different way. In this example, the box has to be recognized as a support rather than as a container— tack the matchbox to the wall, and place the candle upright in the box. The box will catch the falling wax.

A further example is the two-string problem: Knut is left in a room with a pair of pliers and given the task to bind two strings together that are hanging from the ceiling. The problem he faces is that he can never reach both strings at a time because they are just too far away from each other. What can Knut do?

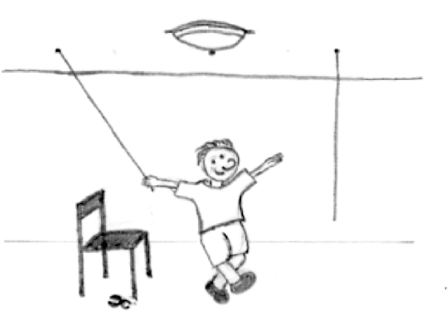
Solution: Knut has to recognize he can use the pliers in a novel function: as weight for a pendulum. He can tie them to one of the strings, push it away, hold the other string and wait for the first one to swing toward him.

MENTAL FIXEDNESS

Functional fixedness as involved in the examples above illustrates a mental set: a person’s tendency to respond to a given task in a manner based on past experience. Because Knut maps an object to a particular function he has difficulty varying the way of use (i.e., pliers as pendulum’s weight).

One approach to studying fixation was to study wrong-answer verbal insight problems. In these probems, people tend to give an incorrect answer when failing to solve a problem rather than to give no answer at all.

A typical example: People are told that on a lake the area covered by water lilies doubles every 24 hours and that it takes 60 days to cover the whole lake. Then they are asked how many days it takes to cover half the lake. The typical response is “30 days” (whereas 59 days is correct).

These wrong solutions are due to an inaccurate interpretation, or representation, of the problem. This can happen because of sloppiness (a quick shallow reading of the problem and/or weak monitoring of their efforts made to come to a solution). In this case error feedback should help people to reconsider the problem features, note the inadequacy of their first answer, and find the correct solution. If, however, people are truly fixated on their incorrect representation, being told the answer is wrong does not help. In a study by P.I. Dallop and

R.L. Dominowski in 1992 these two possibilities were investigated. In approximately one third of the cases error feedback led to right answers, so only approximately one third of the wrong answers were due to inadequate monitoring.

Another approach is the study of examples with and without a preceding analogous task. In cases such like the water-jug task, analogous thinking indeed leads to a correct solution, but to take a different way might make the case much simpler:

Imagine Knut again, this time he is given three jugs with different capacities and is asked to measure the required amount of water. He is not allowed to use anything except the jugs and as much water as he likes. In the first case the sizes are: 127 cups, 21 cups and 3 cups. His goal is to measure 100 cups of water.

In the second case Knut is asked to measure 18 cups from jugs of 39, 15 and 3 cups capacity.

Participants who are given the 100 cup task first choose a complicated way to solve the second task. Participants who did not know about that complex task solved the 18 cup case by just adding three cups to 15.

SOLVING PROBLEMS BY ANALOGY

One special kind of restructuring is analogical problem solving. Here, to find a solution to one problem (i.e., the target problem) an analogous solution to another problem (i.e., the base problem) is presented.

An example for this kind of strategy is the radiation problem posed by K. Duncker in 1945:

As a doctor you have to treat a patient with a malignant, inoperable tumor, buried deep inside the body. There exists a special kind of ray which is harmless at a low intensity, but at sufficiently high intensity is able to destroy the tumor. At such high intensity, however, the ray will also destroy the healthy tissue it passes through on the way to the tumor. What can be done to destroy the tumor while preserving the healthy tissue?

When this question was asked to participants in an experiment, most of them couldn’t come up with the appropriate answer to the problem. Then they were told a story that went something like this:

A general wanted to capture his enemy’s fortress. He gathered a large army to launch a full- scale direct attack, but then learned that all the roads leading directly towards the fortress were blocked by landmines. These roadblocks were designed in such a way that it was possible for small groups of the fortress-owner’s men to pass over them safely, but a large group of men would set them off. The general devised the following plan: He divided his troops into several smaller groups and ordered each of them to march down a different road, timed in such a way that the entire army would reunite exactly when reaching the fortress and could hit with full strength.

Here, the story about the general is the source problem, and the radiation problem is the target problem. The fortress is analogous to the tumor and the big army corresponds to the highly intensive ray. Likewise, a small group of soldiers represents a ray at low intensity. The solution to the problem is to split the ray up, as the general did with his army, and send the now harmless rays towards the tumor from different angles in such a way that they all meet when reaching it. No healthy tissue is damaged but the tumor itself gets destroyed by the ray at its full intensity.

M. Gick and K. Holyoak presented Duncker’s radiation problem to a group of participants in 1980 and 1983. 10 percent of participants were able to solve the problem right away, but 30 percent could solve it when they read the story of the general before. After being given an additional hint — to use the story as help — 75 percent of them solved the problem.

Following these results, Gick and Holyoak concluded that analogical problem solving consists of three steps:

1.  Recognizing that an analogical connection exists between the source and the base problem.

2. Mapping corresponding parts of the two problems onto each other (fortress ® tumour, army ® ray, etc.)

3. Applying the mapping to generate a parallel solution to the target problem (using little groups of soldiers approaching from different directions ® sending several weaker rays from different directions)

Next, Gick and Holyoak started looking for factors that could help the recognizing and mapping processes.

SCHEMAS

The abstract concept that links the target problem with the base problem is called the problem schema. Gick and Holyoak facilitated the activation of a schema with their participants by giving them two stories and asking them to compare and summarize them. This activation of problem schemas is called “schema induction“.

The experimenters had participants read stories that presented problems and their solutions. One story was the above story about the general, and other stories required the same problem schema (i.e., if a heavy force coming from one direction is not suitable, use multiple smaller forces that simultaneously converge on the target). The experimenters manipulated how many of these stories the participants read before the participants were asked to solve the radiation problem. The experiment showed that in order to solve the target problem, reading two stories with analogical problems is more helpful than reading only one story. This evidence suggests that schema induction can be achieved by exposing people to multiple problems with the same problem schema.

HOW DO EXPERTS SOLVE PROBLEMS?

An expert is someone who devotes large amounts of their time and energy to one specific field of interest in which they, subsequently, reach a certain level of mastery. It should not be a surprise that experts tend to be better at solving problems in their field than novices (i.e., people who are beginners or not as well-trained in a field as experts) are. Experts are faster at coming up with solutions and have a higher rate of correct solutions. But what is the difference between the way experts and non-experts solve problems? Research on the nature of expertise has come up with the following conclusions:

1.       Experts know more about their field,

2.      their knowledge is organized differently, and

3.      they spend more time analyzing the problem.

Expertise is domain specific— when it comes to problems that are outside the experts’ domain of expertise, their performance often does not differ from that of novices.

Knowledge: An experiment by Chase and Simon (1973) dealt with the question of how well experts and novices are able to reproduce positions of chess pieces on chess boards after a brief presentation. The results showed that experts were far better at reproducing actual game positions, but that their performance was comparable with that of novices when the chess pieces were arranged randomly on the board. Chase and Simon concluded that the superior performance on actual game positions was due to the ability to recognize familiar patterns: A chess expert has up to 50,000 patterns stored in his memory. In comparison, a good player might know about 1,000 patterns by heart and a novice only few to none at all. This very detailed knowledge is of crucial help when an expert is confronted with a new problem in his field. Still, it is not only the amount of knowledge that makes an expert more successful. Experts also organize their knowledge differently from novices.

Organization: In 1981 M. Chi and her co-workers took a set of 24 physics problems and presented them to a group of physics professors as well as to a group of students with only one semester of physics. The task was to group the problems based on their similarities. The students tended to group the problems based on their surface structure (i.e., similarities of objects used in the problem, such as sketches illustrating the problem), whereas the professors used their deep structure (i.e., the general physical principles that underlie the problems) as criteria. By recognizing the actual structure of a problem experts are able to connect the given task to the relevant knowledge they already have (e.g., another problem they solved earlier which required the same strategy).