10 Chapter 10. Reasoning and Decision-Making

CHAPTER 10: REASONING AND DECISION-MAKING

CHAPTER 10 LICENSE AND ATTRIBUTION
Source: Multiple authors. Memory. In Cognitive Psychology and Cognitive Neuroscience. Wikibooks. Retrieved from https://en.wikibooks.org/wiki/ Cognitive_Psychology_and_Cognitive_Neuroscience
Wikibooks are licensed under the Creative Commons Attribution-ShareAlike License.
Cognitive Psychology and Cognitive Neuroscience is licensed under the GNU Free Documentation License.
Condensed from original version. American spellings used. Content added or changed to reflect American perspective and references. Context and transitions added throughout. Substantially edited, adapted, and (in some parts) rewritten for clarity and course relevance.
Cover photo by Qurratul Ayin Sadia on Unsplash.
Let us consider the following scene of Knut’s life: It is a rainy summer afternoon in Germany and Knut and his wife are tired of watching the black crows in their garden. They decide to escape from the dreary weather and take a vacation to Spain, as Knut and his wife have never been there before. They will leave the next day, and he is packing his bag. He packs the crucial things first: underwear, socks, pajamas, and a toiletry bag with a toothbrush, shampoo, soap, sun tan lotion, and bug spray. Knut cannot find the bug spray, and his wife volunteers to go buy a new bottle. He advises her to take an umbrella for the walk to the pharmacy as it is raining outside, and then he turns back to packing. But what did he already pack into his bag? Immediately, he remembers and continues, putting together outfits and packing his clothing. Since it is summer, Knut packs mostly shorts and t-shirts. After half an hour, he is finally convinced that he has done everything necessary for a nice vacation.
With this story of Knut’s vacation preparation, we will explain the basic principles of reasoning and decision making. We will demonstrate how much cognitive work is necessary for even this fragment of everyday life.
In reasoning, available information is taken into account in the form of premises. A conclusion is reached on the basis of these premises through a process of inference. The content of the conclusion goes beyond either one of the premises. To demonstrate, consider the following consideration Knut makes before planning his vacation:
Premise 1: In all countries in southern Europe it is warm during summer.
Premise 2: Spain is a country in southern Europe.
Conclusion: Therefore, in Spain it is warm during summer.
The conclusion in this example follows directly from the premises, but it includes information that is not explicitly stated in the premises. This is a typical feature of a process of reasoning. We will discuss the two major kinds of reasoning, inductive reasoning and deductive reasoning, which logically complement of one another.
DEDUCTIVE REASONING
Deductive reasoning is concerned with syllogisms in which the conclusion follows logically from the premises. The following example about Knut makes this process clear:
Premise 1: Knut knows: If it is warm, one needs shorts and t-shirts.
Premise 2: He also knows that it is warm in Spain during summer.
Conclusion: Therefore, Knut reasons that he needs shorts and t-shirts in Spain.
In this example it is obvious that the premises are about rather general information, and the resulting conclusion is about a more special case which can be inferred from the two premises. We will now differentiate between the two major kinds of syllogisms: categorical and conditional syllogisms.
CATEGORICAL SYLLOGISMS
In categorical syllogisms, the statements of the premises typically begin with “all”, “none” or “some” and the conclusion starts with “therefore,” “thus,” or “hence.” These kinds of syllogisms describe a relationship between two categories. In the example given above in the introduction of deductive reasoning these categories are Spain and the need for shorts and T- Shirts. Two different approaches serve the study of categorical syllogisms: the normative approach and the descriptive approach.
THE NORMATIVE APPROAC H
The normative approach to categorical syllogisms is based on logic and deals with the problem of categorizing conclusions as either valid or invalid. “Valid” means that the conclusion follows logically from the premises whereas “invalid” means the contrary. Two basic principles and a method called Euler Circles have been developed to help make validity judgments. The first principle was created by Aristotle, and states “If the two premises are true, the conclusion of a valid syllogism must be true” (cp. Goldstein, 2005). The second principle states “The validity of a syllogism is determined only by its form, not its content.” These two principles explain why the following syllogism is (surprisingly) valid:
All flowers are animals. All animals can jump.
Therefore, all flowers can jump.
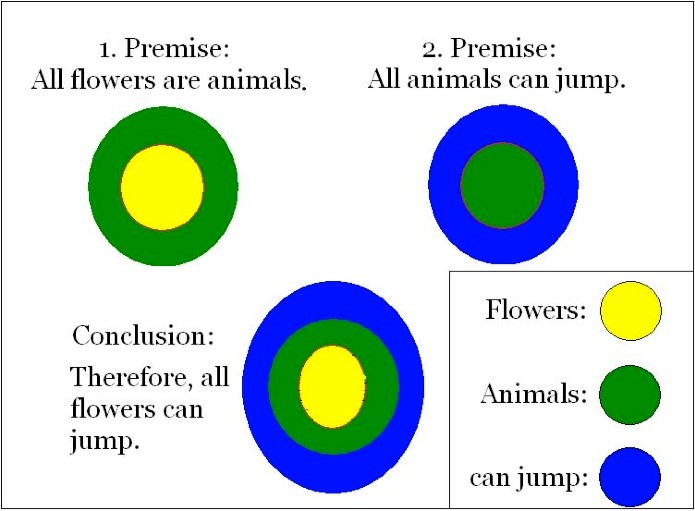
Figure 1. Euler Circles
Even though it is quite obvious that the first premise is not true and further that the conclusion is not true, the whole syllogism is still valid. That is, when you apply formal logic to the syllogism in the example, the conclusion is valid.
It is possible to display a syllogism formally with symbols or letters and explain its relationship graphically with the help of diagrams. One way to demonstrate a premise graphically is to use Euler circles (pronounced “oyler”). Starting with a circle to represent the first premise and adding one or more circles for the second one (Figure 1), one can compare the constructed diagrams with the conclusion. The displayed syllogism in Figure 1 is obviously valid. The conclusion shows that everything that can jump contains animals which again contains flowers. This aligns with the two premises which point out that flowers are animals and thus are able to jump. Euler circles help represent such logic.
THE DESCRIPTIVE APPROAC H
The descriptive approach is concerned with estimating people’s ability to judge the validity of syllogisms and explaining errors people make. This psychological approach uses two methods in order to study people’s performance:
Method of evaluation: People are given two premises and a conclusion. Their task is to judge whether the syllogism is valid.
Method of production: Participants are given two premises. Their task is to develop a logically valid conclusion.
In addition to the form of a syllogism, the content can influence a person’s decision and cause the person to neglect logical thinking. The belief bias states that people tend to judge syllogisms with believable conclusions as valid, while they tend to judge syllogisms with unbelievable conclusions as invalid. Given a conclusion as like “Some bananas are pink”, hardly any participants would judge the syllogism as valid, even though it might be logically valid according to its premises (e.g. Some bananas are fruits. All fruits are pink.)
CONDITIONAL SYLLOGISMS
Another type of syllogism is called “conditional syllogism.” Just like the categorical syllogisms, they also have two premises and a conclusion. The difference is that the first premise has the form “If … then”. Syllogisms like this one are common in everyday life. Consider the following example from the story about Knut:
Premise 1: If it is raining, Knut’s wife needs an umbrella. Premise 2: It is raining.
Conclusion: Therefore, Knut’s wife needs an umbrella.
Conditional syllogisms are typically given in the abstract form: “If p then q”, where “p” is called the antecedent and “q” the consequent.
FORMS OF CONDITIONAL SYLLOGISMS
There are four major forms of conditional syllogisms: modus ponens, modus tollens, denying the antecedent, and affirming the consequent. These are illustrated in the table below (Figure 2) by means of the conditional syllogism above (i.e. If it is raining, Knut’s wife needs an umbrella). The table indicates the premises, the resulting conclusions and whether the form is valid. The bottom row displays the how frequently people correctly identify the validity of the syllogisms.
Figure 2. Different kinds of conditional syllogisms
| Modus Ponens | Modus Tollens | Denying the Antecedent | Affirming the Consequent | |
| Description | The antecedent of the first premise is affirmed in the second premise. | The consequent of the first premise is negated in the second premise. | The antecedent of the first premise is negated in the second premise. | The antecedent of the first premise is affirmed in the second premise. |
|
Formal |
If P then Q. P Therefore Q. |
If P then Q. Not-Q Therefore Not-P. |
If P then Q. Not-P Therefore Not-Q. |
If P then Q. Q Therefore P. |
| Example |
If it is raining, Knut’s wife needs an umbrella. It is raining. Therefore Knut’s wife needs an umbrella. |
If it is raining, Knut’s wife needs an umbrella. Knut’s wife does not need an umbrella. Therefore it is not raining. |
If it is raining, Knut’s wife needs an umbrella. It is not raining. Therefore Knut’s wife does not need an umbrella. |
If it is raining, Knut’s wife needs an umbrella. Knut’s wife needs an umbrella. Therefore it is raining. |
|
Validity |
VALID |
VALID |
INVALID |
INVALID |
|
Correct Judgements |
97% correctly identify as valid. |
60% correctly identify as valid. |
40% correctly identify as invalid. |
40% correctly identify as invalid. |
As we can see, the validity of the syllogisms with valid conclusions is easier to judge correctly than the validity of the syllogisms with invalid conclusions. The conclusion in the instance of the modus ponens is apparently valid. In the example it is very clear that Knut’s wife needs an umbrella if it is raining.
The validity of the modus tollens is more difficult to recognize. Referring to the example, if Knut’s wife does not need an umbrella, it can’t be raining. The first premise says that if it is raining, she needs an umbrella. So, the reason for Knut’s wife not needing an umbrella is that it is not raining. Consequently, the conclusion is valid.
The validity of the remaining two kinds of conditional syllogisms is judged correctly by only 40% of people. If the method of denying the antecedent is applied, the second premise says that it is not raining. But from this fact it does not follow logically that Knut’s wife does not need an umbrella— she could need an umbrella for another reason, such as to shield from the sun.
Affirming the consequent in the case of the given example means that the second premise says that Knut’s wife needs an umbrella, but again the reason for this can be circumstances apart from rain. So, it does not logically follow that it is raining. Therefore, the conclusion of this syllogism is invalid.
The four kinds of syllogisms have shown that it is not always easy to make correct judgments concerning the validity of the conclusions. The following passages will deal with other errors people make during the process of conditional reasoning.
THE WASON SELECTION TASK
The Wason Selection Task is a famous experiment which shows that people make more reasoning errors in abstract situations than when the situation is taken from real life (Wason, 1966).
Figure 3.

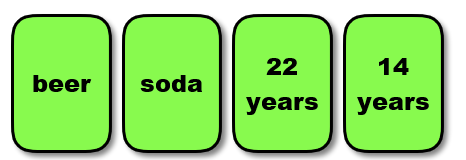
In the abstract version of the Wason Selection Task, four cards are shown to the participants with a letter on one side and a number on the other (Figure 3). The task is to indicate the minimum number of cards that have to be turned over to test whether the following rule is observed: “If there is a vowel on one side then there is an even number on the other side.” 53% of participants selected the ‘E’ card which is correct, because turning this card over is necessary to test the truth of the rule. However another card still needs to be turned over. 64% indicated that the ‘4’ card has to be turned over which is not right. Only 4% of participants answered correctly that the ‘7’ card needs to be turned over in addition to the ‘E’. The correctness of turning over these two cards becomes more obvious if the same task is stated in terms of real-world items instead of vowels and numbers. One of the experiments for determining this was the beer/drinking-age problem used by Richard Griggs and James Cox (1982). This experiment is identical to the
Wason Selection Task except that instead of numbers and letters on the cards, everyday terms (beer, soda and ages) were used (Figure 4). Griggs and Cox gave the following rule to participants: “If a person is drinking beer then he or she must be older than 21.” In this case 73% of participants answered correctly, that the cards with “beer” and “14 years” have to be turned over to test whether the rule is kept.
Figure 4.
Why is the performance better in the case of real–world items?
There are two different approaches to explain why participants’ performance is significantly better in the case of the beer/drinking-age problem than in the abstract version of the Wason Selection Task: the permission schemas approach and the evolutionary approach.
The rule, “if a person is 21 years old or older then they are allowed to drink alcohol,” is well- known as an experience from everyday life. Based on a lifetime of learning rules in which one must satisfy some criteria for permission to perform a specific act, we have a permission schema already stored in long-term memory to think about such situations. Participants can apply this previously-learned permission schema to the Wason Selection Task for real–world items to improve participants’ performance. On the contrary such a permission schema from everyday life does not exist for the abstract version of the Wason Selection Task.
The evolutionary approach concerns the human ability of cheater detection . This approach states that an important aspect of human behavior across our evolutionary history is the ability for people to cooperate in a way that is mutually beneficial. As long as a person who receives a benefit also pays the relevant cost, everything works well in a social exchange. If someone cheats, however, and receives a benefit from others without paying the cost, problems arise. It is assumed that the ability to detect cheaters became a part of the human cognitive makeup during evolution. This cognitive ability improves the performance in the beer/drinking-age version of the Wason Selection Task as it allows people to detect a cheating person who does not behave according to the rule. Cheater-detection does not work in the case of the abstract version of the Wason Selection Task as vowels and numbers cannot behave in any way, much less cheat, and so the cheater detection mechanism is not activated.
INDUCTIVE REASONINGSo far we have discussed deductive reasoning, which is reaching conclusions based on logical rules applied to a set of premises. However, many problems cannot be represented in a way that would make it possible to use these rules to come to a conclusion. Inductive reasoning is the process of making observations and applying those observations via generalization to a different problem. Therefore one infers from a special case to the general principle, which is just the opposite of the procedure of deductive reasoning. A good example of inductive reasoning is the following:
Premise: All crows Knut and his wife have ever seen are black.
Conclusion: Therefore, they reason that all crows on earth are black.
In this example it is obvious that Knut and his wife infer from the simple observation about the crows they have seen to the general principle about all crows. Considering the figure above, this means that they infer from the subset (yellow circle) to the whole (blue circle). As with this example, it is typical in inductive reasoning that the premises are believed to support the conclusion, but do not ensure the conclusion.
Figure 6.

FO R M S O F I N D U C T I V E R E A S O N I N G
The two different forms of inductive reasoning are “strong” and “weak” induction. The former indicates that the truth of the conclusion is very likely if the assumed premises are true. An example for this form of reasoning is the one given in the previous section. In this case it is obvious that the premise (“All crows Knut and his wife have ever seen are black”) gives good evidence for the conclusion (“All crows on earth are black”) to be true.
Nevertheless it is still possible, although very unlikely, that not all crows are black.
On the contrary, conclusions reached by “weak induction” are supported by the premises in a relatively weak manner. In this approach, the truth of the premises makes the truth of the conclusion possible, but not likely. An example for this kind of reasoning is the following:
Premise: Knut always listens to music with his iPhone.
Conclusion: Therefore, he reasons that all music is only heard with iPhones.
In this instance the conclusion is obviously false. The information the premise contains is not very representative and although it is true, it does not give decisive evidence for the truth of the conclusion.
To sum it up, strong inductive reasoning yields conclusions which are very probable whereas the conclusions reached through weak inductive reasoning are unlikely to be true.
RELIABILITY OF CONCLUSIONS
If the strength of the conclusion of an inductive argument has to be determined, three factors concerning the premises play a decisive role. The of Knut and his wife’s observations about crows (see previous sections) displays these factors:
When Knut and his wife observe, in addition to the black crows in Germany, the crows in Spain, the number of observations they make concerning the crows increases. Furthermore, the representativeness of these observations is supported if Knut and his wife observe the crows at different times and in different places and see that they are black every time.
The quality of the evidence for all crows being black increases if Knut and his wife add scientific measurements that support the conclusion. For example, they could find out that the crows’ genes determine that the only color they can be is black.
Conclusions reached through a process of inductive reasoning are never definitely true, as no one has seen all crows on earth. It is possible, although very unlikely, that there is a green or brown exemplar. The three above factors contribute to the strength of an inductive argument. The stronger these factors are, the more reliable the conclusions reached through induction.
PROCESSES AND CONSTRAINTS
In a process of inductive reasoning, people often make use of certain heuristics. These heuristics often help people make adequate conclusions, but sometimes may cause errors. In the following sections, two of these heuristics (availability heuristic and representativeness heuristic) are explained. Subsequently, the confirmation bias is introduced, which can influence people to use their own opinions in reasoning without realizing it.
THE AVAILABILIT Y HEURISTIC
Things that are more easily remembered are judged to be more prevalent. An example of this is an experiment done by Lichtenstein et al. (1978).
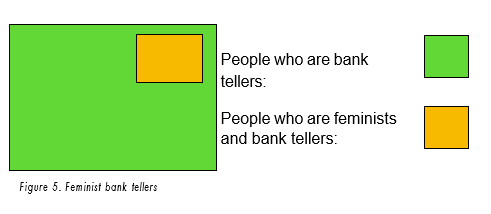
Figure 5. Feminist bank tellers
People who are bank tellers:
People who are feminists and bank tellers:
Participants were asked to choose from a list which causes of death occur most often. Because of the availability heuristic people, judged more “spectacular” causes like homicide or tornadoes to cause more deaths than others, like asthma. The reason for this is that, for example, films and news in television are very often about spectacular and interesting causes of death. This is why this information is more readily available to the subjects in the experiment.
Another effect of the availability heuristic is called illusory correlations. People tend to judge according to stereotypes. It seems to them that there are correlations between certain events which in reality do not exist— this is what is known as “prejudice.” Usually a correlation seems to exist between negative features and a certain class of people. If, for example, one’s neighbor is jobless and very lazy one tends to correlate these two attributes and create the prejudice that all jobless people are lazy. This illusory correlation occurs because one takes into account information which is available and judges this to be prevalent in many cases.
THE REPRESENTATIVENESS HEURISTIC
If people have to judge the probability of an event, they try to find a comparable event and assume that the two events have a similar probability. Amos Tversky and Daniel Kahneman (1974) presented the following task to their participants in an experiment: “We randomly chose a man from the population of the U.S., Robert, who wears glasses, speaks quietly and reads a lot. Is it more likely that he is a librarian or a farmer?” More of the participants answered that Robert is a librarian, which is an effect of the representativeness heuristic.
Participants compared the description of Robert with the typical depiction of a librarian, and found that the description was more like a librarian than a farmer. So, the event of a typical librarian is more comparable with Robert than the event of a typical farmer. Of course this effect may lead to errors, as Robert is randomly chosen from the population and as it is perfectly possible that he is a farmer even though he speaks quietly and wears glasses.
The representativeness heuristic also leads to errors in reasoning in cases where the conjunction rule is violated. This rule states that the conjunction of two events is never more likely to be the case than the single events alone. An example for this is the case of the feminist bank teller (Tversky & Kahneman, 1983). If we are introduced to a woman who is very interested in women’s rights and has participated in many political activities in college, and we are to decide whether it is more likely that she is a bank teller or a feminist bank teller, we are drawn to conclude the latter as the facts we have learned about her resemble the event of a feminist bank teller more than the event of only being a bank teller.
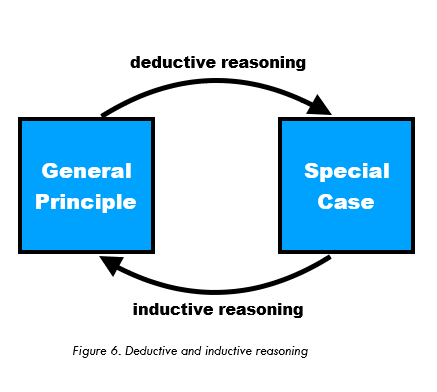
Figure 6. Deductive and inductive reasoning
However, it is in fact more likely that somebody is just a bank teller than it is that someone is a feminist in addition to being a bank teller. This effect is illustrated in Figure 5, where the green square, which stands for just being a bank teller, is much larger and thus more probable than the smaller orange square, which displays the conjunction of bank tellers and feminists, which is a subset of bank tellers.
CONFIRMATION BIAS
People tend to use what they believe to be true or good to when using evidence to make inferences. If, for example, someone believes that they have bad luck on Friday the thirteenth, they will especially look for every negative event on this particular date but will be inattentive to negative events on other days. This behavior strengthens the belief that there exists a relationship between Friday the thirteenth and having bad luck. This example shows that all information is not equally taken into account to come to a conclusion, but rather on seeks out information which supports one’s own belief. This effect leads to errors as people tend to reason in a subjective manner, if personal interests and beliefs are involved.
All the mentioned factors influence the subjective probability of an event so that it differs from the actual probability (probability heuristic). Of course all of these factors do not always appear alone, but they influence one another and can occur in combination during the process of reasoning.
INDUCTION VS DEDUCTION
The table below (Figure 7) summarizes the most prevalent properties and differences between deductive and inductive reasoning which are important to keep in mind.
Figure 7. Induction vs. deduction
| Deductive Reasoning | Inductive Reasoning | |
| Premises | Stated as facts or general principles (“It is warm in the Summer in Spain.”) | Based on observations of specific cases (“All crows Knut and his wife have seen are black.”) |
|
Conclusion |
Conclusion is more special than the information the premises provide. It is reached directly by applying logical rules to the premises. |
Conclusion is more general than the information the premises provide. It is reached by generalizing the premises’ information. |
|
Validity |
If the premises are true, the conclusion must be true. |
If the premises are true, the conclusion is probably true. |
|
Usage |
More difficult to use (mainly in logical problems). One needs facts which are definitely true. |
Used often in everyday life (fast and easy). Evidence is used instead of proved facts. |
DECISION MAKINGThe psychological process of decision making is critical in everyday daily life. Imagine Knut deciding between packing more blue or more green shirts for his vacation (which would only have minor consequences) but also about applying a specific job or having children with his wife (which would have important consequences in his future life).
There are three different ways to analyze decision making. The normative approach assumes a rational decision-maker with well-defined preferences. The descriptive approach is based on empirical observations and on experimental studies of choice behavior. The prescriptive approach develops methods to improve decision making.
MISLEADING EFFECTS
People may struggle to make the “right” decision because of different misleading effects, which mainly arise because of the constraints of inductive reasoning. In general this means that our model of a situation or problem might not be ideal to solve it in an optimal way.
One misleading effect is the so-called focusing illusion. By considering only the most obvious aspects of a situation to make a decision, people often neglect more important aspects. For example, in considering job offers in different locations, a person may pay too much attention to salient aspects of a location such as weather, and relatively less to highly important aspects such as circumstances at work.
The way a problem is framed can evoke different decision strategies. If a problem is framed in terms of gains, people tend to use a risk-aversion strategy, while framing a problem in terms of losses leads to a risk-taking strategy. An example of the same problem and predictably different choices is the following experiment: A group of people is asked to imagine themselves $300 richer than they are. They are then confronted with the choice of a sure gain of $100 or an equal chance to gain $200 or nothing. Most people avoid the risk and take the sure gain, which means they take the risk-aversion strategy. Alternatively, if people are asked to assume themselves to be $500 richer than in reality, given the options of a sure loss of $100 or an equal chance to lose $200 or nothing, the majority opts for the risk of losing $200, which represents a risk-taking strategy. This phenomenon is known as a framing effect and can also be illustrated by figure 8 above, which shows a concave function for gains and a convex one for losses. (Foundations of Cognitive Psychology, Levitin, D. J., 2002)
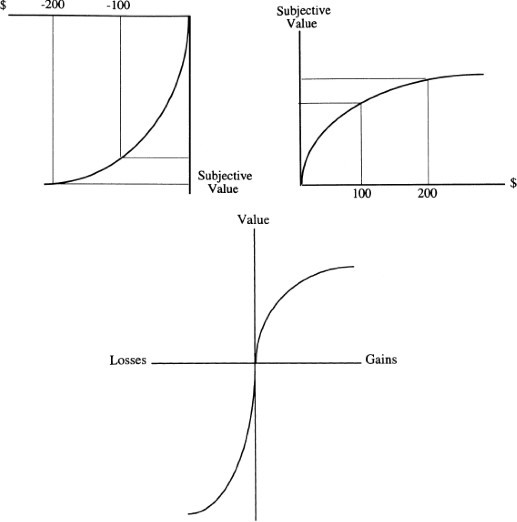
Figure 8. Relation between (monetary) gains/losses and their subjective value according to Prospect Theory
REFERENCES
_________________________________________________________________________________________________________________________________________________________
Krawczyk,Daniel (2018). Reasoning: The Neuroscience of How We Think. Elsevier.
Goldstein, E. Bruce (2005). Cognitive Psychology – Connecting, Mind Research, and Everyday Experience. Thomson Wadsworth.
Marie T. Banich (1997). Neuropsychology. The neural bases of Mental Function. Houghton Mifflin.
Wilson, Robert A.& Keil, Frank C. (1999). The MIT Encyclopedia of the Cognitive Sciences. Massachusetts: Bradford Book.
Ward, Jamie (2006). The Student’s Guide To Cognitive Science. Psychology Press. Levitin, D. J.(2002). Foundations of Cognitve Psychology.
Schmalhofer, Franz. Slides from the course: Cognitive Psychology and Neuropsychology, Summer Term 2006/2007, University of Osnabrueck

